接上文，如果没有看到上面的同学，请先点击阅读“”。

(3) 不确定度及测量结果表达式

现在考虑一个终极问题：人们在使用测量数据时，在无法获得真值的约束下，对数据可靠性的实际要求是什么？

分析一个数据可靠性要求较高的例子：螺母和螺钉在不同的机床上批量生产，其尺寸必须严格匹配，否则螺母和螺钉不能一起使用。 假设我们现在知道螺杆的外径是5.43厘米，那么螺母的内径也一定是5.43厘米。 但螺杆、螺母的直径测量存在误差，加工时也会出现产品尺寸与预期不一致等问题。 工程师如何处理这个问题呢？ 他们发现直径在5.40~5.47（即5.43±0.03）厘米范围内的螺钉和螺母可以一起使用。 因此，他们不需要知道螺钉和螺母的直径是否正好等于5.43厘米。 在质量检验过程中，他们测量生产的螺钉和螺母，直径在5.42至5.44厘米范围内被认为是合格的，必须包装并运走。 超出此范围的螺钉和螺母被视为废品，必须重新制造。 （为了简化说明，本示例与实际项目有所不同，但原理是完全一样的）

因此，在实际使用数据时，人们并不关心真实值到底等于多少，只需要知道真实值在足够小的范围内即可。 在科学技术中，用不确定性（英文）来表达这个范围。 直观含义：不确定性是指无法确定真实值的程度。 例如，就上述螺钉和螺母而言：5.43 cm 为平均值，0.03 cm 为不确定度，螺钉和螺母的直径在 5.43 ± 0.03 cm 范围内变化。

举个例子，让你对不确定性有更深入的理解：

你的一位马达哈室友去上课了，但他把手机落在宿舍了，让你帮他拿去。 他的手机在办公桌的第二个抽屉里，距抽屉左侧15.6厘米，距抽屉外侧5.7厘米（这是手机位置的真实值）。

场景一：他直接告诉你具体位置，让你帮他接电话。 你可能会觉得他有问题：有必要这么精确吗？ ------这说明真值往往不被关心甚至令人讨厌！

第二种情况：他告诉你手机放在他办公桌的第二个抽屉里。 这时，就意味着真实值是未知的，但是真实值的变化范围是已知的。 手机位置的不确定性是整个抽屉。 打开抽屉后即可使用手机。 -----这就是不确定性恰到好处时的美妙感觉。

第三种情况：他的马达哈问题继续出现，他只告诉你把电话放在他的桌子上。 这时候手机位置变化的幅度就更大了，也就是不确定性变大了，变成了整个桌子。 你必须翻遍整个桌子才能找到你的手机。 ------当你焦急地寻找手机时，你就会充分明白什么是不确定性。

第四种情况：他根本不记得自己的手机是落在宿舍还是食堂，所以他让你帮他找到并带回来。 不管你们关系多好，你还是会考虑要不要帮他这个忙。 -----用迂腐的语言来描述这件事：不确定性太大，以至于整个数据都失去了意义！

这个例子也说明了不确定性只需要满足使用要求即可。 不需要太小，但也不能太大。

看完例子相信你会明白，为了满足数据实际使用的要求，需要满足两点：（1）尽可能接近真实值的平均值； (2)满足不确定性的使用要求。

要求(1)很容易满足。 将所有重复的测量数据相加，然后除以测量数据的数量，得到平均值。 只要测量次数足够，平均值就可以非常接近真实值。

对于如何满足要求（2），概率论和数理统计发现，正态分布曲线与标准差σ有以下重要关系（推导过程略），如图4所示：

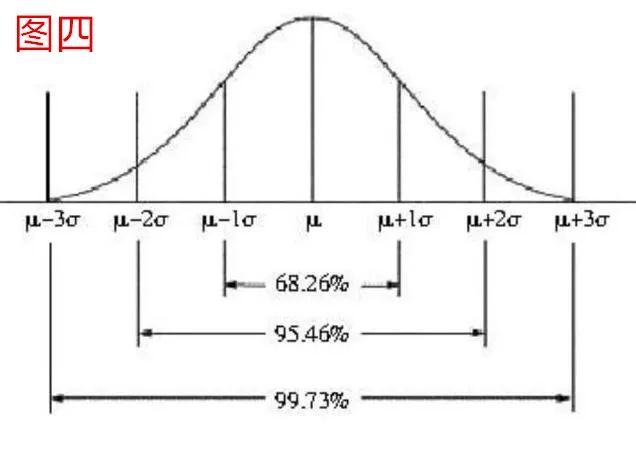
测量值在μ-1σ~μ+1σ之间的概率为68.26%，在μ-3σ~μ+3σ之间的概率为99.73%。 这意味着：在知道标准差σ之后，您可以根据σ值使用μ。 该值界定了一个以中心为中心的区间。 当区间变大时，测量值（当然也包括真值）落在该区间内的概率就越大。 该概率称为置信概率。 关键是这个区间不需要很大。 例如，如果区间在 μ-2σ~μ+2σ 之间，则真值有 95.46% 的概率位于该区间内，而超出该范围的可能性极小（小于 5% 的概率）。

68.26% 的概率太小，这意味着真实值大约有 30% 的机会落在指定范围之外。 虽然99.73%意味着真实值很有可能落在指定范围内，但它并不比95.46%大多少。 但代价是数据变异范围大了50%（3σ相比2σ），这显然不划算。 所以最好的选择是95.46%。 这也是大学物理实验中约定的置信概率（95%）。 也就是说，默认情况下，我们对测量数据取值范围的要求只要求真实值有95%的概率落在这个范围内。 不需要 百分之一百都在这个范围内。

那么我们是否可以重复测量5到10次，然后计算平均值μ，然后根据标准差σ的计算公式计算出σ值，然后用μ±2σ来表示测量结果呢？

等等，根据上面的分析，标准差是一个有能力但不可靠的产品，时不时就会掉链子。 怎么处理呢？ 物理学家有一个办法：找到一个可靠的合作伙伴。

找谁比较好？ 回想一下，上面的有效数字中有一个重要的结论：仪器的最小刻度值越小，仪器的测量精度越高，测量数据与真实值的偏差越小，可靠性越高的数据。 它与标准差属性相同。 越小，测量数据的可靠性越高。 实践中也是如此。 当我们测量数据时，在最小尺度值范围内确实无法准确估计真实值。

但我们能否直接用μ±（σ+最小刻度值）来表示测量结果呢？ 决不！ 过于简单粗暴，并不能保证真实值有95%的概率落在这个区间内。

这件事该如何处理呢？

物理学家问数学家：兄弟，我知道最小尺度值必须和标准差匹配，但是怎么匹配，请给我一个方案！

数学家拿出笔记本算了算，得出结论：最小刻度值的一半不能直接相加，最小刻度值的一半比较好。 而且，不能直接添加。 它必须像毕达哥拉斯定理一样被“添加”。 那是

物理学家：其他一切都很容易解释。 我有一个问题，为什么在最小刻度值的一半时如此准确？

数学家：因为我是根据理想的完美测量仪器来计算的。

物理学家：你不觉得我会穷一辈子做学术，仪器也会老化损坏吗？ 而且我年纪大了，手也慢了。 测量其他物理量很容易。 测量时间的时候，我看到要按手表，但是如果真的按的话，可能会慢一点。 你不想想吗？

数学家：好吧，那你说了算！ 理想的是最小比例值的一半。 大家可以根据自己的情况稍微修改一下。 无论如何，这都是概率。 概率的意思是一样的，可以适当改变。

物理学家：我明白了！

物理学家回到家后，深思熟虑后向弟子们宣布：

正常情况下，如果仪器没有发现问题，使用

(测量结果表达)

代替 μ±2σ，表示测量结果并表明真实值有 95% 的概率在此范围内。

但是，如果仪器有点不可靠，或者测量器有点不可靠，我们可以根据实际情况扩大一点。 我们不需要使用最小比例值的一半，而是使用最小比例值，甚至更大。 为了表达方便，我们规定以下行话（就是术语！）：

由于情况的复杂性，术语“最小分度值的一半”由仪器误差限Δ仪表代替。 它表示仪器示值与真值之间可能出现的最大误差的绝对值。 当仪器正常时，默认值为仪器最小刻度值的一半，但您可以根据测量情况进行一些更改（大学物理实验就是这样做的）。 此时，测量结果的表达式变为

由于实际情况可能比这个复杂一点（本科阶段基本不会遇到那种复杂），所以可以用更广泛的概念来表示：

标准差一词扩展到统计不确定性。 所有通过统计方法计算出的分量都包含在这一类中，称为A类不确定性，用UA表示（当然大学物理实验都是标准差σ）；

术语 Δmeter 被扩展到通过其他方法获得的不确定度。 顾名思义，除了通过统计方法获得的以外的一切都包含在这一类中，称为B型不确定性，用UB表示（大多数大学物理实验都是Δmeter）。

这样，我们要寻找的不确定性就是它们的综合结果，即：

至此，我们得到了不确定度概念下测量结果的结果表达式：

该式表示被测物理量X的真实值落在

位于该区间内的概率为 95%。

对于用户来说，得到这个测量结果后，不仅知道了测量值的大小，而且知道了它的变化范围，可以放心地使用你的测量数据。

数据格式的原因和规则

根据误差理论，制定有效数字、绝对误差和相对误差以及不确定性数据的舍入规则：

我们将测量结果分为两类（两部分）：

（1）表示物理量大小的部分称为被测量，包括直接被测量和间接被测量（需要通过直接被测量函数运算得到）；

(2)表示误差大小的误差量，包括绝对误差、相对误差和不确定度。

它们的舍入规则不同。

计量数量的四舍五入规则是，小于五则四舍五入，等于五则四舍五入，大于五则四舍五入。 这样做的原因是为了让舍入和舍入的概率相等，使得舍入后测量的量不会变大或变小。

然而，误差量是不同的，并且误差量的舍入规则都是非零的。 制定理由如上图4所示。 当不确定度比实际值增加一点时，只会使真实值更有可能落入测量表达式所表示的区间内。 影响并不显着。 然而，如果不进一步，而是丢弃的话，真实值可能落在测量表达式表示的区间内，也可能落在测量表达式表示的区间之外，导致表达式混乱，使用不便，所以它不能被丢弃，只有当它非零时才能输入。 一。

绝对误差也是如此。

至于相对误差如果也是非零的话，是有原因的：相对误差*真值=绝对误差，且平均值±绝对误差=真值区间。 相对误差应该更大，即真实值范围应该更大，这意味着不确定性更大。

在数据格式方面，有效数字、绝对误差和相对误差、不确定度和测量结果表达均受有效数字的影响，作为误差分析的依据：

有效号码格式为一个可靠号码+一个可疑号码+单位； 例如：5.46 厘米。

在存在绝对误差或不确定度的情况下，测量结果的表达式为：平均值±绝对误差/不确定度+单位。 为了满足（至少形式上）最后一位是可疑数而其余数是可靠数的要求，我们规定对于绝对误差和不确定性只能保留一位有效数字。

例如：

5.46±0.03厘米，那么5.4是可靠的，0.06是可疑的，因为它在0.03~0.09之间波动；

但如果绝对误差和不确定度保留2位有效数字，例如：5.46±0.13厘米，那么显然0.46是一个可疑数，不符合有效数字的要求。

但如果出现5.46±0.09厘米怎么办？ 这确实会导致 0.46 成为一个可疑的数字。 此时只能说正式满足了最后一位数字是可疑数字的要求。

在最终结果表达式中，平均值的最后一位必须与绝对误差或不确定性对齐。 例如，上例中的5.46±0.03厘米，不确定度在百分位处，平均值的最后一位也必须保留在百分位处。 不能有更多的分位数，因为平均值的剩余部分是无效数字。

这里经常发生的情况是，在计算平均值时，严格遵循有效数字的计算和保留规则，但得到的结果却远远超出了不确定性。 此时，多余的部分必须根据计量数量进行修整。 消除输入规则以获得与不确定性一致的结果。 例如：上面计算平均值得到的结果是5.4574，不确定度是0.03。 那么写成5.4574±0.03的测量结果一定是错误的，因为5.45的最后一位数字已经很可疑了。 最后的数字 0.0074 更加不可靠，必须删除。

对于相对误差保留一到两位有效数字也是如此。 保留更多的零件是没有意义的。

中间计算过程不能夸大数据的可靠性，也不能降低数据的可靠性。 因此，我们要求计算过程中出现的数据比通常规则下保留多一位有效数字。 不能少也不能多。 如果数量过多，则必须采用其他方法来确定最终结果是否满足一个可靠数+一个可疑数（包括形式上）的要求。

至此，我们已经利用错误理论揭示了数据格式的内在逻辑关系并得出了其规律。

更详细的数据格式内容和示例，请点击阅读“”。

总结

有效数字作为最基本的要求，定性地反映了测量数据的可靠性； 由于人们要求定量评价测量数据与真值的偏差，因此就产生了绝对误差和相对误差； 随着人们对误差现象认识的加深，在系统分析误差来源和深入了解误差规律后，提出了不确定度的概念，并提出了符合数据实际使用要求的测量结果的表达方式。获得。

因此，从认识的发展过程来看，从有效数字、绝对误差、相对误差到不确定性的发展，是一个从直观观察到理论分析深化认识的过程；

就评估测量数据质量的有效性而言，它们从粗略表达到精细分析的进展；

从三者评价测量数据质量的地位来看，有效数字是最基本的。 所有测量必须满足有效数字的要求，所有误差分析必须以有效数字为依据； 对误差的大小有一个定量的了解。 绝对误差和相对误差仅在必要时才需要计算； 仅当需要测量数据的可靠性时才使用不确定度。

作为一名大学生，无论是毕业后工作还是继续读研，都面临着处理实际问题的要求，所以必须对这三者有深入的掌握并熟练运用。 这是大学物理实验必须掌握的基础知识和基本技能。

其他问题及解答

问题一：大学物理实验中，是否需要每次实验都计算不确定度？

答：从上面我们可以知道，答案是否定的。 注意每个实验中的有效数字，因为它是最基本的。 只有当需要更准确地了解测量对象数据的误差大小和变化范围时，才需要计算不确定度。 此外，计算不确定度必须满足一定的条件： (1) 可以进行重复测量； (2) 仪器误差限已知。 值 Δ 米。

由于大多数大学物理实验都具备计算不确定性的条件，而为了训练大家分析数据的能力，很多实验都需要计算不确定性。

问题2：绝对误差、相对误差和不确定度的舍入规则均为非零，会导致计算结果不准确。 这不是违背了我们做事严谨的要求吗？

答：其实绝对误差、相对误差，尤其是不确定性，它们本质上都是估计量。 由于无法得知真实值，因此使用真实值计算出的绝对误差和相对误差是估计值； 由于标准差仅使用有限数量的测量数据来计算，因此A类不确定度本身很可能偏离真实情况。 凭经验确定的仪器误差限 Δ 和仪器确定的 B 类不确定度也是估计值，因此不确定度也是估计值，而不是精确的量。 因此，在计算绝对误差、相对误差和不确定度时，按照规则计算即可。 如果一定要强调准确性，那就与实际情况不相符。

问题三：本文的知识体系与大部分教材的知识体系不一致。 我应该相信哪一个？

答：一般教材的写作风格是从不确定性的概念出发，借助严格的数学推导推导其他内容。 这种方式的优点是地位高。 占据了不确定性的高度之后，就可以借助数学严格推演其他内容。 概念和结论都无可挑剔（事实上，没有人攻击它），但它也有缺点。 数学不好，概率论没掌握。 学数理统计的学生很多，学起来很痛苦。

写这篇文章的思路是从简单的有效数字开始，根据人们对误差分析认识逐渐加深、对数据可靠性和质量评估要求逐步提高的客观发展过程，再开发其他内容。 当然，没有通用的教科书可以做到这一点。 它如此严谨，但好处是符合人们认识客观世界的过程。 适合初学者掌握误差分析的基本概念和总体框架，具有浓郁的物理气息。

读完本文，您将完全具备大学物理实验中的误差分析和数据处理能力。 对于一些有学习余地的同学，可以在学完概率论、数理统计之后再回顾一下教材的推导过程。 你会发现我文章的概念性结论和其他内容都和课本上的一样。 不过，对于大多数学生来说，不建议花费大量精力使用概率论和数理统计来分析实验误差。 没有必要。